Union-Find 算法（并查集）

本文最后更新于：2023年11月4日 下午

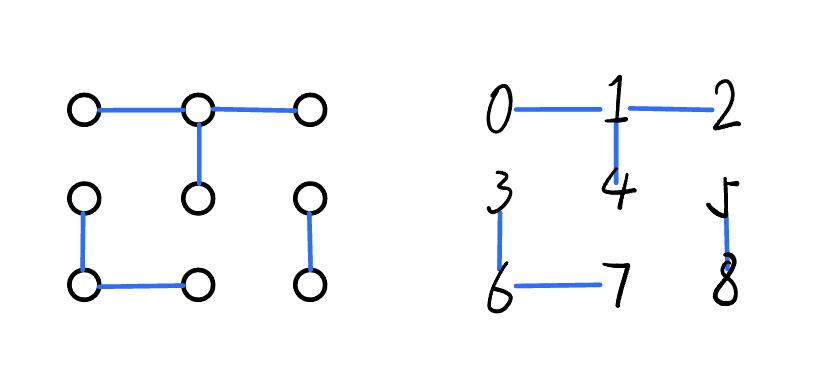
问题描述

Union-Find 算法用于确定网络中任意给定的两个触点是否相通。这样说可能不好理解，所以让我们通过一个简单的问题来了解一下它。
看到下面这张图，图上有九个点，现在任意给出两个点，我们需要快速判断这两个点是否相连，或者说这两个点是否相通，有什么好办法吗？

为了更好理解这个问题，我们可以将九个点转化为 0-8 这九个数字，并把其当成一个数组来看待，然后再假设问题的输入就是一些元组，如(1, 4)，就代表 1 和 4 之间是连通的。
就以上面图为参考，我们想要知道相邻的两个点是否连通是很容易的，比如 0 和 1；但是，如果想要知道 0 和 4 是否是连通的，该用什么方法呢？对输入进行dfs或是bfs吗？那太复杂了，毕竟我们不需要给出两点间的详细路径，只需要知道两者是否连通，没必要浪费资源，所以我们需要换种思路。

Union-Find 算法的 API

为此，我们需要先为这个算法设计一些 API，这些操作既可以处理输入，也能够解决问题。下面给出UnionFind类的基本框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class UnionFind
{
	private int[]? _id;
	private int _count;

	/// <summary>
	/// 以整数标识（0 到 N-1）初始化 N 个触点
	/// </summary>
	/// <param name="N"></param>
	public UnionFind(int N)
	{
		_count = N;
		_id = new int[N];
		for (int i = 0; i < N; i++)
		{
			_id[i] = i;
		}
	}

	/// <summary>
	/// 连通分量的数量
	/// </summary>
	/// <returns></returns>
	public int Count()
	{
		return _count;
	}

	/// <summary>
	/// 如果 p 和 q 存在于同一个（连通）分量中则返回 true
	/// </summary>
	/// <param name="p"></param>
	/// <param name="q"></param>
	/// <returns></returns>
	public bool Connected(int p, int q)
	{
		return Find(p) == Find(q);
	}

	/// <summary>
	/// p 所在的分量的标识符
	/// </summary>
	/// <param name="p"></param>
	/// <returns></returns>
	public int Find(int p)
	{
		throw new NotImplementedException();
	}

	/// <summary>
	/// 在 p 和 q 之间添加一条连接
	/// </summary>
	/// <param name="p"></param>
	/// <param name="q"></param>
	public void Union(int p, int q)
	{
		throw new NotImplementedException();
	}
}

可以看到框架中有两个方法还未实现，这两个方法其实正是这个算法的关键，而我们接下来要干的事就是实现这两个方法。

Union 和 Find 方法的实现

quick-find 算法

该算法的思路就是保证当且仅当id[p]等于id[q]时p和q是连通的，换句话说，在同一个连通分量里的所有触点在id[]中的值必须全部相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public uint Find(uint p)
{
	// quick-find
	return _id![p];
}

public void Union(uint p, uint q)
{
	// quick-find
	// 将 p 和 q 归并到相同的连通分量中
	uint pId = Find(p);
	uint qId = Find(q);
	// 如果 p 和 q 已经在相同分量中则不需要采取任何行动
	if (pId == qId) { return; }
	// 将 p 的分量重命名为 q 的分量
	for (uint i = 0; i < _id!.Length; i++)
	{
		if (_id[i] == pId) { _id[i] = qId; }
	}
	_count--;
}

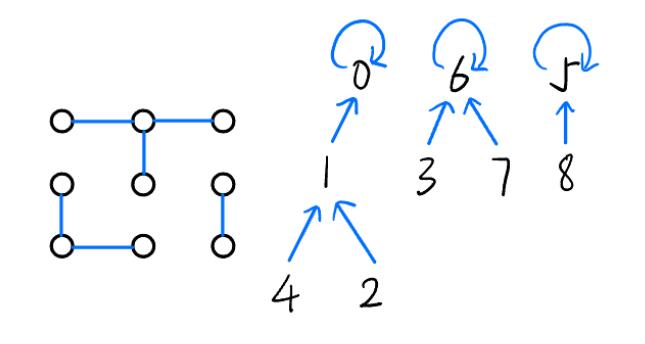
quick-union 算法

这个算法的思路其实就是通过构造森林来确定连通分量和两个触点是否相连。下面的图将有助于理解该算法：

也就是说，我们调用Find方法的话，应该沿着其找到其所在分量的标识符，也就是根触点。而调用Union方法对p和q进行归并的话，就利用Find方法找到两个触点的根触点，若不同，更改其中一个根触点的标识符为另一个根触点即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public uint Find(uint p)
{
	// quick-union
	while (p != _id![p])
	{
		p = _id[p];
	}
	return p;
}

public void Union(uint p, uint q)
{
	// quick union
	// 找到两个触点的根触点
	uint pRoot = Find(p);
	uint qRoot = Find(q);
	// 如果 p 和 q 的根触点相同，说明在同一棵树下（换句话说，在相同分量中）
	if (pRoot == qRoot) { return; }
	// 否则合并两棵树
	_id![pRoot] = qRoot;
	_count--;
}

Union 和 Find 方法的优化

加权quick-union

当然，普通的quick-union算法是不会判断树的大小的，所以可能会出现一颗大树归并到小树上，或者出现更糟糕的情况：0链接到1，1链接到2，如此下去。
那么，为了改进我们的union方法，我们现在需要记录一下每棵树的大小，并且总是将小树连接到大树上。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
public class WeightedUnionFind
{
	private uint[] _id;  // 以触点作为索引
	private uint _count;  // 连通分量的数量
	private int[] _size;  // 各个根节点所对应的分量的大小

	/// <summary>
	/// 以整数标识（0 到 N-1）初始化 N 个触点
	/// </summary>
	/// <param name="N"></param>
	public WeightedUnionFind(uint N)
	{
		_count = N;
		_id = new uint[N];
		_size = new int[N];
		for (uint i = 0; i < N; i++)
		{
			_id[i] = i;
			_size[i] = 1;
		}
	}

	/// <summary>
	/// 连通分量的数量
	/// </summary>
	/// <returns></returns>
	public uint Count()
	{
		return _count;
	}

	/// <summary>
	/// 如果 p 和 q 存在于同一个（连通）分量中则返回 true
	/// </summary>
	/// <param name="p"></param>
	/// <param name="q"></param>
	/// <returns></returns>
	public bool Connected(uint p, uint q)
	{
		return Find(p) == Find(q);
	}

	/// <summary>
	/// p 所在的分量的标识符
	/// </summary>
	/// <param name="p"></param>
	/// <returns></returns>
	public uint Find(uint p)
	{
		// quick-union
		while (p != _id[p])
		{
			p = _id[p];
		}
		return p;
	}

	/// <summary>
	/// 在 p 和 q 之间添加一条连接
	/// </summary>
	/// <param name="p"></param>
	/// <param name="q"></param>
	public void Union(uint p, uint q)
	{
		// quick union
		// 找到两个触点的根触点
		uint pRoot = Find(p);
		uint qRoot = Find(q);
		// 如果 p 和 q 的根触点相同，说明在同一棵树下（换句话说，在相同分量中）
		if (pRoot == qRoot) { return; }
		// 否则将小树合并到大树上
		if (_size[pRoot] < _size[qRoot])
		{
			_id[p] = q;
			_size[qRoot] += _size[pRoot];
		}
		else
		{
			_id[q] = p;
			_size[pRoot] += _size[qRoot];
		}
		_count--;
	}
}

路径压缩

理想情况下，我们希望每个节点都直接链接到它的根节点上。为了实现这种理想情况，只需要为Find()添加一个循环，将在路径上遇到的所有节点都直接链接到根节点。这样我们所得到的结果是几乎完全扁平化的树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
public class WeightedPathCompressUnionFind
{
    private uint[] _id;  // 以触点作为索引
    private uint _count;  // 连通分量的数量
    private int[] _size;  // 各个根节点所对应的分量的大小

    /// <summary>
    /// 以整数标识（0 到 N-1）初始化 N 个触点
    /// </summary>
    /// <param name="N"></param>
    public WeightedPathCompressUnionFind(uint N)
    {
        _count = N;
        _id = new uint[N];
        _size = new int[N];
        for (uint i = 0; i < N; i++)
        {
            _id[i] = i;
            _size[i] = 1;
        }
    }

    /// <summary>
    /// 连通分量的数量
    /// </summary>
    /// <returns></returns>
    public uint Count()
    {
        return _count;
    }

    /// <summary>
    /// 如果 p 和 q 存在于同一个（连通）分量中则返回 true
    /// </summary>
    /// <param name="p"></param>
    /// <param name="q"></param>
    /// <returns></returns>
    public bool Connected(uint p, uint q)
    {
        return Find(p) == Find(q);
    }

    /// <summary>
    /// p 所在的分量的标识符
    /// </summary>
    /// <param name="p"></param>
    /// <returns></returns>
    public uint Find(uint p)
    {
        // 找到根节点
        uint root = p;
        while (root != _id[root])
        {
            root = _id[root];
        }
        // 路径上所有节点直接链接到根节点上
        while (p != root)
        {
            uint temp = _id[p];
            _id[p] = root;
            p = temp;
        }
        return p;
    }

    /// <summary>
    /// 在 p 和 q 之间添加一条连接
    /// </summary>
    /// <param name="p"></param>
    /// <param name="q"></param>
    public void Union(uint p, uint q)
    {
        // 找到两个触点的根触点
        uint pRoot = Find(p);
        uint qRoot = Find(q);
        // 如果 p 和 q 的根触点相同，说明在同一棵树下（换句话说，在相同分量中）
        if (pRoot == qRoot) { return; }
        // 否则将小树合并到大树上
        if (_size[pRoot] < _size[qRoot])
        {
            _id[p] = q;
            _size[qRoot] += _size[pRoot];
        }
        else
        {
            _id[q] = p;
            _size[pRoot] += _size[qRoot];
        }
        _count--;
    }
}

编写的测试方法

本来想说实现一下读取文件的，但是搁置了（逃

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
void UnionFindTest()
{
    // 读取触点数量并初始化 N 个分量
    uint N = 9;
    try
    {
        Console.WriteLine("Please enter a number(e.g: 9):");
        N = UInt32.Parse(Console.ReadLine());
    }
    catch (FormatException)
    {
        Console.WriteLine("Please enter a correct number.");
        return;
    }
    UnionFind unionFind = new UnionFind(N);

    // 建立触点间的连接
    Console.WriteLine("Please enter p and q(e.g: 1 4):");
    string? numbers = "";
    while (!string.IsNullOrEmpty(numbers = Console.ReadLine()))
    {
        try
        {
            uint[] tmp = Array.ConvertAll(numbers.Split(" "), uint.Parse);
            if (tmp.Length != 2 || tmp[0] >= N || tmp[1] >= N)
            {
                Console.WriteLine("Please check your input.(Wrong format)");
                continue;
            }
            uint p = tmp[0];
            uint q = tmp[1];
            if (unionFind.Connected(p, q)) { continue; }
            unionFind.Union(p, q);
        }
        catch
        {
            Console.WriteLine("Please check your input.(Not a num)");
        }
    }

    // 打印连通分量数
    Console.WriteLine(unionFind.Count() + " components.");
}

这里有一只爱丽丝

希望本文章能够帮到您~

Solution
#C# #并查集
Union-Find 算法（并查集）
https://map1e-g.github.io/2023/10/29/algorithm-union-find/
作者
MaP1e-G
发布于
2023年10月29日
许可协议