初级排序介绍

本文最后更新于：2023年11月24日 晚上

修改声明

代码于 2023/11/19 号进行了“重构”。

排序算法类模板

该类定义一些排序算法会用到的辅助方法，例如：less和exch方法。前者对元素进行比较，后者交换元素位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public class Sorts<T> where T : IComparable<T>
{
    /// <summary>
    /// 待实现的排序方法
    /// </summary>
    /// <param name="a"></param>
    public static void Sort(T[] a) { }

    /// <summary>
    /// 对元素进行比较，若 a1 小于 a2 则返回 true
    /// </summary>
    /// <param name="a1"></param>
    /// <param name="a2"></param>
    /// <returns></returns>
    protected static bool Less(T a1, T a2)
    {
        return a1.CompareTo(a2) < 0;
    }

    /// <summary>
    /// 交换两个元素的位置
    /// </summary>
    /// <param name="a"></param>
    /// <param name="index1"></param>
    /// <param name="index2"></param>
    protected static void Exch(T[] a, int index1, int index2)
    {
        var temp = a[index1];
        a[index1] = a[index2];
        a[index2] = temp;
    }

    /// <summary>
    /// 打印数据
    /// </summary>
    /// <param name="a"></param>
    public static void Show(T[] a)
    {
        for (int i = 0; i < a.Length; i++)
        {
            Console.Write(a[i] + " ");
        }
        Console.WriteLine();
    }

    /// <summary>
    /// 检查数组是否有序
    /// </summary>
    /// <param name="a"></param>
    /// <returns></returns>
    public static bool IsSoreted(T[] a)
    {
        for (int i = 1; i < a.Length; i++)
        {
            if (Less(a[i], a[i - 1]))
            {
                return false;
            }
        }
        return true;
    }
}

冒泡排序

冒泡排序的基本思想就是：每一趟遍历，都反复比较相邻元素，然后把最大的元素放到数组最后面（保持数组a[a.Length - i...a.Length]有序）。
冒泡排序是稳定的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Bubble<T> : Sorts<T> where T : IComparable<T>
{
    public static new void Sort(T[] a)
    {
        bool swapped;  // 检测内层循环中是否进行过交换
        for (int i = 0; i< a.Length; i++)
        {
            swapped = false;
            for (int j = i; j < a.Length - 1; j++)
            {
                if (Less(a[j + 1], a[j]))  // 如果后一个元素小于前面一个元素，则对两个元素进行交换
                {
                    Exch(a, j, j + 1);
                    if (!swapped)
                    {
                        swapped = true;
                    }
                }
            }
            if (!swapped)  // 如果一次内循环都没有进行过交换，说明数组已经是有序的了
            {
                return;
            }
        }
    }
}

选择排序

选择排序的基本思想：首先，找到数组中最小的那个元素，其次，将它和数组的第一个元素交换位置。再次，在剩下的元素中找到最小的元素，将它与数组的第二个元素进行交换。如此反复，直到将整个数组排序。
选择排序是稳定的。
选择排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Selection<T> : Sorts<T> where T : IComparable<T>
{
    public static new void Sort(T[] a)
    {
        for (int i = 0; i < a.Length; i++)
        {   // 将 a[i] 和 a[i + 1]...a[a.Length]中的最小元素进行交换
            int min = i;  // 最小元素的索引
            for (int j = i + 1; j < a.Length - 1; j++)
            {
                if (Less(a[j], a[min]))
                {
                    min = j;
                }
            }
            Exch(a, i, min);
        }
    }
}

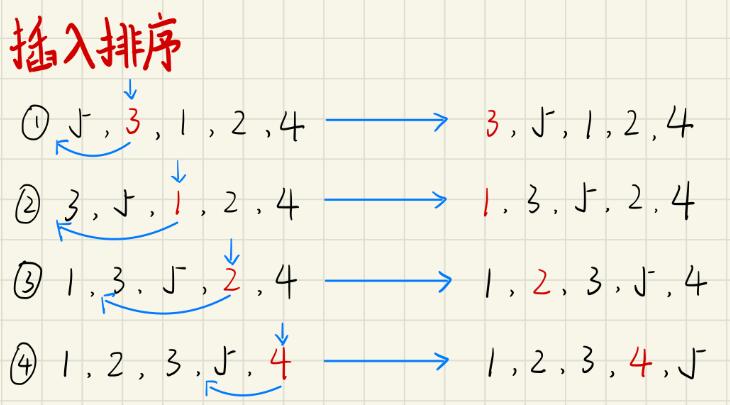
插入排序

插入排序的基本思想：从数组的第二个数开始，将它插入到其左边数组中的合适位置，保持左边的数组一直是有序状态，直至数组遍历完成，整个数组都为有序状态。
插入排序是稳定的。
插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Insertion<T> : Sorts<T> where T: IComparable<T>
{
    public static new void Sort(T[] a)
    {
        for (int i = 1; i < a.Length; i++)
        {   // 将 a[i] 插入到 a[i - 1]，a[i - 2]，a[i - 3]...中
            for (int j = i; j > 0 && Less(a[j], a[j - 1]); j--)
            {
                Exch(a, j, j - 1);
            }
        }
    }
}

要对插入排序进行改进，只需要在内循环中将较大的元素向右移动，而不是每次都进行交换，就能减少一半的数组访问次数，改进后的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class InsertionImproved<T> : Sorts<T> where T : IComparable<T>
{
    public static new void Sort(T[] a)
    {
        int n = a.Length;

        // 找哨兵
        int min = 0;
        for (int i = 1; i < n; i++)
        {
            if (Less(a[i], a[min]))
            {
                min = i;
            }
        }
        Exch(a, min, 0);

        // 减少了一半交换
        for (int i = 2; i < n; i++)
        {
            T temp = a[i];
            int j = i;
            while (Less(temp, a[j - 1]))
            {
                a[j] = a[j - 1];
                j--;
            }
            a[j] = temp;
        }
    }
}

希尔排序

希尔排序其实就是改进过的插入排序，因为插入排序只交换相邻的元素，如果一个很小的元素排在很后面，就需要进行很多次移动，所以希尔排序的思想就是先对数组进行局部排序，交换不相邻的元素，保持数组局部有序，最后再进行一次插入排序来完成排序。

希尔排序的思想是使数组中任意间隔为 h 的元素都是有序的。这样的数组被称为 h 有序数组。换句话说，一个 h 有序数组就是 h 个互相独立的有序子数组编织在一起组成的一个数组。在进行排序时，如果 h 很大，我们就能将元素移动到很远的地方，为实现更小的 h 有序创造方便。
希尔排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Shell<T> : Sorts<T> where T : IComparable<T>
{
    public static new void Sort(T[] a)
    {
        int n = a.Length;
        int h = 1;
        while (h < n / 3) { h = h * 3 + 1; }  // 1, 4, 13, 40, 121, 364, 1093, ...
        while (h >= 1)
        {   // 将数组变为 h 有序
            for (int i = h; i < n; i++)
            {   // 将 a[i] 插入到 a[i - h]，a[i - 2*h]，a[i - 3*h]...中
                for (int j = i; j >= h && Less(a[j], a[j - h]); j -= h)
                {
                    Exch(a, j, j - h);
                }
            }
            h /= 3;
        }

    }
}

编写的测试方法

算法模板类提供了一个IsSorted方法来判断数组是否有序，可以用Debug.Assert来进行测试，不过我这里没用：Debug.Assert(!Sorts.IsSoreted(a), "数组不是有序的");

这里有一只爱丽丝

希望本文章能够帮到您~

Solution
#C# #选择排序 #插入排序 #希尔排序
初级排序介绍
https://map1e-g.github.io/2023/10/29/algorithm-elementary-sorts/
作者
MaP1e-G
发布于
2023年10月29日
许可协议